Static Code Analysis of a Storage Tank’s Shell with Bumps out of Design Code
Problem definition
Static Code Analysis’ Goal
To determine the behavior of a limestone’s slurry tank for CT that contains geometric imperfections -documented in topographic protocol and NC report- out of design code API650.
Using API579-1/ASME-FFS-1 methodology.
Imperfections
Tank dimensions: Ø20.5x15m. Assembling and welding imperfections with deviations up to +35 /-75mm on the theoretical perimeter.

Methodology
Nonlinear static analysis
Nonlinear geometric static analysis to identify stresses and deformations of the structure as a result of the application of static charges and contour known conditions. This analysis allows to model the geometric imperfections and obtain the resistance response, implicitly including the instability testing (local or generalized buckling) by numerical convergence of the analysis.

API 579-1/ASME FFS-1 Validation:
Limitation of stress. Equivalent Allowable Stress Criteria
- Categorization of stress.
- Acceptability of stress.
Limitation of deformation (arrow)
Limitation of buckling
It has been considered additionally to the operating charges such as own weight,
shaker charge and hydrostatic pressure, pressure by wind (EC 27 m / s) and snow (EC).
Conclusions
Geometric imperfections according to topographic protocol does not compromise the structural safety of the structure.
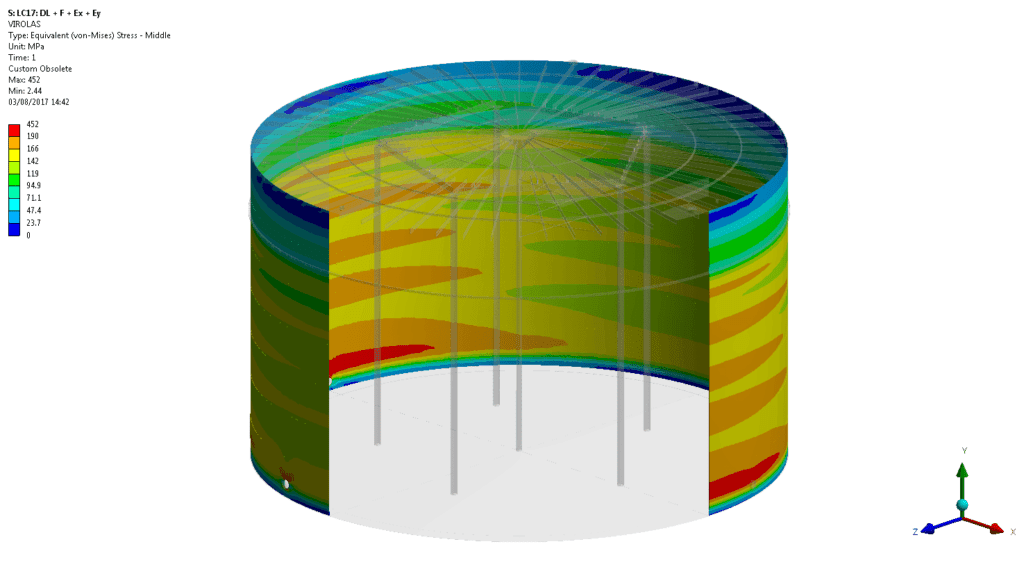
Based on the results of resistance to plastic failure obtained, it is concluded that the shell has sufficient safety margin against failure by excessive plasticization because it doesn’t exceed in any case the stress limits specified by code API579-1/ASME FFS-1.
- In the worst-case scenario, for the hypothesis of 0.9P + Ps + D L +0.75 +0.75 +0.75 W Ss, the primary membrane stress is 159.9MPa, being the allowable up to 160MPa
Regarding the results of the stability analysis, it is concluded that the shell has a sufficient safety margin against instability according to the limits specified by API579-1/ASME FFS-1 Code.
Buckling coefficients are higher than 10 compared to an allowable of 9.66 for instability caused by axial compression, and an allowable of 2.5 for instability caused by external pressure.